
The Norilsk Nickel Harjavalta Oy plant in Finland
How Nonlinear Modeling Improved Understanding of a Hydrometallurgical Leaching Process
Development of quality mathematical models fit for industrial production processes, particularly leaching, has been considered to be very difficult. However, the results of a recent project illustrate that newer nonlinear modeling techniques have clearly improved the situation.
By Abhay Bulsari, Esa Lindell, Rauno Luoma and Tuomo Laukkanen

This article describes the experience of developing nonlinear models of a leaching process used by Norilsk Nickel Harjavalta Oy in Harjavalta, Finland. Theoretical issues are also discussed, followed by a brief explanation of how the nonlinear models were implemented in software suitable for use by plant operators.
Norilsk Nickel Harjavalta Oy has years of experience in producing high-quality nickel products, including both metals and chemicals, and several of its products are produced by innovative and efficient production processes developed in-house. The company’s product portfolio is diverse, its products have applications in several industrial sectors and are exported to practically all parts of the world from the Harjavalta plant. Even so, its production processes are in continuous development.
The Process Development
Problem
Any production process can be made
more efficient with better quantitative
knowledge of the effects of process
variables and feed characteristics on
the consequences of the process.
Different industrial processes have different characteristics—different objectives, variables, constraints, raw materials or micro-organisms. The process may be a batch process, a con-tinuous process or a fed-batch one. However, some things are common to process development of various kinds of processes. A product needs to be pro-duced with a given process, from speci-fied raw materials such that the result-ing product properties satisfy some con-ditions, typically upper and lower limits.
a1< property 1 < b1
a2< property 2 < b2
a3< property 3 < b3
…
an< property n < bn
For development of many kinds of industrial processes, product concen-trations, concentrations of undesired side-products and viscosity, for exam-ple, can be considered to be the prod-uct properties, where the products are the materials (liquid, solid, gas, slurry) resulting at the end of the process. Besides these constraints, there also are limits on other variables. Process variables such as temperatures, pres-sures, flow rates or pH stirring, for example; and feed characteristics such as concentrations in the feed and parti-cle sizes also have upper and lower lim-its. The objective of process develop-ment is usually to determine the best values of the feed characteristics and process variables such that the product properties are within desired limits, and preferably, a production economic vari-able (e.g., production rate, raw materi-al consumption, energy efficiency, puri-ty, number of defects or emissions, to name a few) is maximized or mini-mized. The same methodology can be applied to a wide variety of processes.
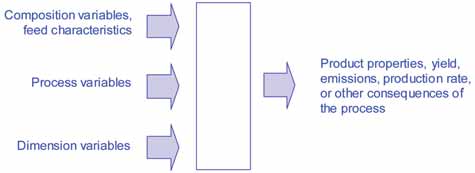
The degrees of freedom may differ in different cases. Sometimes there may be no control over the raw material or feed characteristics, and the only degrees of freedom may be the process variables within certain limits. Sometimes, different amounts of feed materials may be degrees of freedom. The problem looks somewhat similar from the process modeling point of view for a wide variety of industrial process-es. From the process modeling point of view, the product properties are conse-quences of feed characteristics, process variables and dimension variables, as summarized in the figure above.
These relations, however, tend to be complicated for most industrial processes in general, and mineral leaching processes in particular. Mathematical modeling can be per-formed in various ways, and different ways are suitable in different situa-tions. Attempts at physical modeling lead to modest accuracies in predicting most of the interesting consequences of leaching like product purity and energy consumption, partly because they require plenty of assumptions and sim-plifications, and partly because of lack of knowledge of mass transfer charac-teristics and reaction kinetics of sever-al components in leaching. Empirical and semi-empirical models, on the other hand, have neither of these limi-tations. All that is needed is sufficient amount of production data with a fair variation in the variables of interest.
Nonlinear Modeling
Nonlinear modeling has been success-fully utilized by many sectors of indus-tries for a variety of purposes
1,2
, partic-ularly for process development involv-ing metallurgy
3-5
, polymers
6
, plastics
processing7,8
, ceramics
9
, concrete
10
,
pulp, paper and board, power genera-tion
11
, semiconductor processing
12
,
water treatment, chemical produc-tion
13
, biotechnology
14
and food pro-cessing. Yet, overall industry awareness
of these techniques is still very limited.
Nonlinear modeling can roughly be defined as empirical or semi-empirical modeling which takes at least some nonlinearities into account. Nonlinear models can be static or dynamic. Nonlinear modeling can be performed in many ways. The simpler ways include polynomial regression and linear regres-sion with nonlinear terms. Nonlinear regression is useful in some situations. The form of the nonlinearities, however, has to be specified in these older tech-niques. The newer techniques of non-linear modeling are based on free-form nonlinearities. They include series of basis functions, splines, kernel regres-sion, feed-forward neural networks, etc. Feed-forward neural networks are a set of efficient tools for nonlinear model-ing, particularly because of their uni-versal approximation capability. 15
Why Nonlinear Modeling?
Mathematical models represent knowl-edge of quantitative effects of relevant
variables in a concise and precise form.
They can be used instead of experimen-tation if they are reliable enough.
Mathematical models also permit the
user to carry out various kinds of calculations such as optimization, which can
be used to determine suitable values of
process variables. Mathematical model-ing can be performed in various ways,
and different ways are suitable in different situations.
It is not possible to use physical modeling in every situation. Even if it is possible, physical models tend to com-pute the output more slowly than empirical or semi-empirical models. Development of physical models is time consuming. Nonlinear modeling tends to be expensive, but physical modeling usually costs even more. Physical mod-els involve assumptions and simplifica-tions. Thus, empirical modeling is often a better alternative.
Traditional empirical modeling is based on linear statistical techniques. But, nothing in nature is absolutely lin-ear, so it helps to take nonlinearities into account rather than ignore them. If the range of variables is small, linear techniques are sometimes sufficient. New techniques of nonlinear modeling based on artificial neural networks allow us to approximate nonlinearities without specifying in detail the nonlin-earities to be accounted for. They allow for free-form nonlinearities, unlike lin-ear and nonlinear regression methods.
For this work, we used an empirical approach based on feed-forward neural networks, since plenty of reliable pro-duction data was available from the plant. Such networks are a set of effi-cient tools for nonlinear modeling, par-ticularly because of their universal approximation capability.
Feed-forward Neural
Networks
Feed-forward neural networks consist of
neurons or nodes, which are calculation
units. These neurons are arranged in
layers, and the connections between
neurons are in the forward direction
only; i.e., from the input layer toward
the output layer, as shown in the figure
below. The input layer has as many
neurons as the number of input vari-ables and usually the neurons in the
input layer serve only to provide the
value to several neurons in the layer
above it. There can be layers between
the input and the output layers, which
are called hidden layers. The neurons in
the hidden layer normally have some
nonlinearity. In most situations, only
one hidden layer is used.
The output of each neuron i in a feed-forward neural network is given by
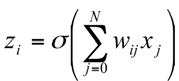
where the activation function σ(a) is often the logistic sigmoid, given by
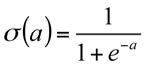
The incoming signals to the neuron
are x
j
, and wij are the weights for each
connection from the incoming signals
to the i
th
neuron. The wi0 terms are
called biases. This results in a set of
algebraic equations which relate the
input variables to the output variables.
For each observation (a set of input and
output variables), the outputs can be
predicted from these equations based
on a given set of weights. The training
procedure aims at determining the
weights which result in the smallest
sum of squares of prediction errors.
There are a number of well-known
methods for achieving this, which is
basically an optimization problem; we
generally use the Levenberg-Marquardt
method. It is also possible to combine
neural networks with physical models or
other empirical models, which often
lead to better solutions.
Quality of Nonlinear
Models
Many people claim to be able to devel-op nonlinear models in the form of neu-ral networks or others. A large number
of people can offer impressive user
interfaces that hide the details of the
models inside. However, not many peo-ple can solve real-world problems. Very
few are able to produce industrially
usable systems of good quality. Fewer
are consistently successful in every
project they agree to undertake. The
result is that there is a wide variation in
the quality of nonlinear models.
2 How
do you know which models are good
and which models are not? In other
words, what are the characteristics that
you look for in a good nonlinear model?
The simple answer is that ‘the proof of the pudding is in the eating’: A good model has to work. There is, of course, more to it than that. A good model for industrial purposes has to be reliable. Accuracy is secondary. A good industrial model has to be robust and easily updatable. Models should have some trans-parency, and the simpler the better.
A good model efficiently treats all the important nonlinearities. Reliability, robustness, simplicity, maintainability often come at the cost of accuracy and efficient treatment of nonlinearities. These conflicting demands make non-linear modeling a harder task. That does not leave many people who will offer you all these attributes. Most are satisfied with claiming accuracy. It is important to insist on highly reliable and robust models because several decisions might be made based on the answers from these models. Considering the possible effects these decisions can have, it becomes quite obvious that the models should be as high quality as possible.
In other words, the quality of a non-linear model is much more than accura-cy, and there is a scarcity of quality of nonlinear modeling today. There are no simple ways of measuring reliability and robustness of nonlinear models. How does one ensure these and other fea-tures? Experience and expertise are essential for neural network model development. However, a good software tool also goes a long way by offering a variety of measures that highlight possi-ble undesirable features in the models.
Nonlinear Models for the
Leaching Process
For the development of nonlinear mod-els of Norilsk Nickel’s leaching process,
a large number of variables were identi-fied. Production data from July 9,
2010, to January 22, 2012, were available for use.
The data set contained 53 columns of different variables. Production data tends to be dilute in information and often contains misleading observations. Therefore, only selected observations from this data were taken for model development. Although this work was done carefully, several observations had to be excluded from the ‘cleaner’ data set during model development work. Nonlinear models were developed for several consequences of the process, including nickel content in the leachate, some impurities in the leachate, nickel content in the other stream and yield.
Implementation of the
Nonlinear Models for
Efficient Use
Mathematical models can contain a lot
of valuable quantitative knowledge in a
concise and a precise manner. Concrete
benefits, however, are achieved only if
the models are used efficiently, but
plant operators cannot be expected to
understand nonlinear models—and
even most R&D personnel cannot work
with the equations of nonlinear models,
which tend to be unwieldy and cumber-some for mathematical operations.
Therefore, LUMET systems have been
developed over 15 years with several
features which make it easier for the
user to utilize the model for several
kinds of calculations. LUMET systems
are a set of software components offer-ing facile use of the models by people
unfamiliar with nonlinear modeling. For
this leaching process, nonlinear models
were implemented in a LUMET system.
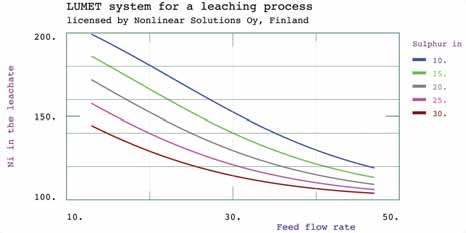
When implemented in LUMET sys-tems, we can use the models to see the individual and combined effects of the input variables on each of the outputs. The accompanying figure illustrates the effect of feed flow rate at different sul-phur contents in the feed on nickel con-tent in the leachate. At low sulphur contents in the feed, nickel content in the leachate is more sensitive to the feed flow rate. The figure below shows contours of yield in terms of feed flow rate and temperature in a certain loca-tion in the autoclave. One can see that there is an optimal feed flow rate which varies with that temperature.
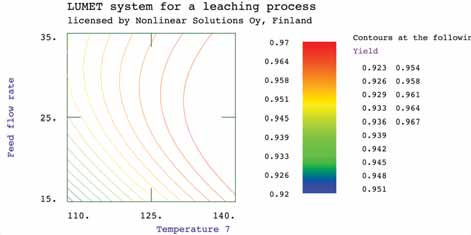
Contours of yield in terms of feed flow rate and temperature in a certain location in the autoclave.

Nickel cathodes, briquettes and powder.
Some input variables have desirable effects on some outputs while having undesirable effects on other outputs. These and such other conflicting objec-tives make it a challenging task to determine the best ways of operating the autoclave. LUMET systems make that task easier.
Boosting Business
Competitiveness with
Nonlinear Modeling
Any process operation can be made
more efficient with better quantitative
knowledge of the effects of process
variables and feed characteristics on
the consequences of the process. These
relationships, however, tend to be com-plicated for most industrial processes.
Nonlinear modeling is a relatively new technology which helps production units derive more from their equipment and raw materials while also improving their control over product properties. Industries usually collect a lot of pro-duction data that is unused or under-utilized—data that can contain valu-able information which can be extract-ed by nonlinear modeling. If used effec-tively, nonlinear modeling can add to a company’s competitiveness.
Nonlinear modeling can contribute much to mining and mineral process-ing. New technologies come up from time to time which affect production economics, and open up new possibili-ties. Those companies that utilize new technologies effectively have an edge over those that do not. Nonlinear mod-eling is expensive compared with linear statistical techniques, but as experi-ence shows time and again, the benefits clearly outweigh the costs.
Scientists and engineers can per-form better process development with less experimentation effort by using nonlinear modeling. Deriving maximum mileage from a reactor or separation equipment is an optimization task, for which it is necessary to have detailed quantitative knowledge of its operation. Such knowledge can be summarized in the form of nonlinear empirical or semi-empirical models describing the effects of process variables and feed character-istics. It has become feasible to utilize this new technology in practice.
Development of quality mathemati-cal models fit for industrial production processes, particularly leaching, has been considered to be very difficult. However, newer nonlinear modeling techniques have clearly improved this situation, as results from this work demonstrate. Because these nonlinear models can be quite complicated, and technical personnel generally aren’t experts on optimization techniques, a simple tool has been devised bringing these new possibilities within the reach of engineers and scientists.
References
1. A. Bulsari (ed.), Neural Networks for Chemical Engineers, Elsevier, Amsterdam, 1995.
2. A. Bulsari, “Quality of nonlinear modeling in process industries.” Internal Report NLS/1998/2.
3. A. Bulsari et al., “Uuden sukupolven laatujärjestelmät sisältävät epälin-eaarisia malleja,” Vuoriteollisuus, No. 1/1999, 38-41.
4. A. Bulsari, I. Vuoristo and I. Koppinen, “How nonlinear models help improve quality of wire rods of a copper alloy,” Wire and Cable Technology International (January 2011) 96-99.
5. A. Bulsari, H. Keife and J. Geluk, “Nonlinear models provide better control of annealed brass strip microstructure,” Advanced Materials and Processes(July 2012) 18-20.
6. A. Bulsari et al., “Nonlinear model-ing paves the way to bespoke poly-mers,” British Plastics and Rubber, December 2002, 4-5.
7. A. Bulsari and M. Lahti, “How non-linear models help improve the pro-duction economics of extrusion pro-cesses,” British Plastics and Rubber (September 2008) 30-32.
8. A. Bulsari and M. Lahti, “Nonlinear models guide secondary coating of OFCs,” Wire and Cable Technology International, Vol. 29, No. 5 (September 2001) 40-43.
9. A. Bulsari et al., “Correlation of in vitro and in vivo dissolution behav-iour of stone wools using nonlinear modeling techniques,” Journal of the European Ceramic Society, Vol. 27, No. 2-3 (2007) 1837-1841.
10. A. Bulsari, H. Kylmämetsä and K. Juvas, “Nonlinear models of work-ability and compressive strength help minimise costs,” Concrete Plant International, No. 6 (Decem-ber 2009) 36-42.
11. A. Bulsari, A. Wemberg, A. Anttila and A. Multas, “Improving com-bustion efficiency,” World Coal, Vol. 18, No. 6 (June 2009) 35-40.
12. A. Bulsari and V.-M. Airaksinen, “Nonlinear models used to address epi layer uniformity,” Solid State Technology, Vol. 47, No. 7 (July 2004) 33-38.
13. A. Bulsari, T. Saarenko, J. Valtanen and L. Kaskinen, “Nonlinear models enhance distillation,” Chemical Processing, Vol. 74, No. 10 (October 2011) 43-46.
14. A. Bulsari et al., “Speeding develop-ment of an enantioselective enzy-matic process for a pharmaceutical intermediate,” BioProcess International, Vol. 5, No. 8 (September 2007) 52-64.
15. Hornik, K., Stinchcombe, M. and White, H., “Multilayer feedforward networks are universal approxi-mators,” Neural Networks, Vol. 2, (1989) 359-366.
16. P. E. Gill, W. Murray and M. H. Wright, Practical Optimisation, Academic Press, London (1981) 136-140.
As a docent in the chemical engineering department until 2003, Abhay Bulsari (abulsari@abo.fi) taught and con-ducted research at Åbo Akademi University. He has taught courses on nonlinear modeling and neural networks for process industries, and currently is affiliated with Nonlinear Solutions Oy, Turku, Finland. Esa Lindell (esa.lin-dell@nornik.fi) is R&D director, Rauno Luoma (rauno.luoma@ nornik.fi) is R&D manager and Tuomo Laukkanen (tuomo.laukkanen@nornik.fi) is a re-search engineer at Norilsk Nickel Harjavalta Oy.